GPS - Da irrt die Maus

am
Leider lassen sich Klausuren nicht vermeiden (△ Klausuren bringen nichts). Und die Geheimniskrämerei einiger Kollegen um die, ach so heiligen, Klausuren mache ich nicht mit. Die Studierenden haben sowieso einen Rechtsanspruch auf Einsichtnahme auch auf Kopie [1]. Also bin ich immer auf der Suche nach neuen Ideen.

Für die Telematik-Vorlesung ist natürlich das GPS relevant. Viele Dinge erklären die Sachgeschichten in der ↪ Sendung mit der Maus sehr gut. 2007 hat Ralph Caspers die Funktion eines ↪ Navigationssystems erklärt. 

Das ist sicherlich kindgerecht.
Aber ist sie auch richtig?
Also habe ich daraus eine Klausuraufgabe gemacht.
  • Nehmen Sie Stellung, in wie weit Herr Caspers die Funktion des Global Positioning Systems vereinfacht, richtig oder ggf nicht korrekt darstellt.
  • Erklären Sie dabei auch, wie Entfernungen zu Satelliten gemessen werden und wie daraus Koordinaten berechnet werden. Prüfen Sie jede einzelne Aussage des Textes.
  • Welche Annahmen stecken in der Darstellung?


Die Redaktion hat mich darauf hingewiesen,
 dass das Video nicht eingebunden werden darf.
Danke dafür.
Das Google-Orakel findet heute mehr als 200 Videos
Suchbegriff: "Sendung mit der Maus" Navigationssystem
Update vom 6.7.20 aufgrund der Antwort der Mausredaktion 


Zur Bearbeitung habe ich das für die Studierenden transskibiert:

[Text überspringen]."Vorher weiß der, wo ich gerade bin? Ich kann Straßenschilder lesen. Aber was kann der Computer lesen? Woher weiß er wo ich stehe? Der Computer bekommt Hilfe, von ganz weit oben. 

Das hier ist unsere Erde – also, im Modell natürlich nur. Und mitten in Deutschland steht mein Auto auch im Modell. 

Und wo ist die Hilfe? Das ist die Hilfe, oder zumindest ein Teil. Das ist ein Satellit. Von diesen Satelliten fliegen ziemlich viele um die Erde herum. Und diese Satelliten helfen dem Navigationssystem. Das geht so: 

Auf der Erde steht das Auto mit dem Navigationssystem und weit über der Erde, da ist der Satellit im Weltall und dieser Satellit funkt ein Signal. Und dieses Signal wird vom Navigationssystem empfangen. Das ist so ähnlich wie ein Radiosender allerdings nur für Navigationssysteme. 

Und aus diesem Signal errechnet der Computer im Navigationssystem wieweit der Satellit vom Navigationssystem entfernt ist. Das ist ungefähr dann, diese Strecke hier. Das Problem ist, damit weiß man noch lange nicht wo man auf der Erde ist. Denn es gibt auf der Erde ganz, ganz viele Orte, die genau dieselbe Entfernung zum Satelliten haben. Hier auf diesem Kreis Dieser ganze Kreis, Alle diese Punkte sind gleich weit vom Satelliten entfernt. 

Deshalb gibt es einen zweiten Satelliten. Und auch hier ist es wieder so: der Computer im Auto, der weiß ganz genau wie weit dieser zweite Satellit von dem Auto entfernt ist. Und auch hier gibt's wieder genau wie beim ersten viele, viele Punkte auf der Erde, die genauso weit von diesen Satelliten entfernt sind. Und es gibt jetzt aber zwei Punkte, wo sich diese Kreise treffen. Die überschneiden sich da und das bedeutet: das Auto kann entweder hier an diesem ersten Punkt sein oder hier an diesem zweiten Punkt. 

Um das zu finden, wo das Auto jetzt tatsächlich ist, gibt es einen dritten Satelliten. Und da passiert genau das gleiche: das Auto weiß ganz genau wie weit es von den Satelliten entfernt ist. Und natürlich gibt es auch hier wieder ganz viele Punkte, die diese Entfernung zum Satelliten haben. 


Aber es gibt auf der ganzen Welt nur einen einzigen Punkt, wo sich diese drei Kreise von diesen drei Satelliten treffen. Und genau das ist der Ort, wo das Auto ist. Und dieser vierter Satellit ist noch mal zur Kontrolle, dass alle Berechnungen richtig sind. Dank der Satelliten 1-2-3-4, weiß der Computer im Auto ganz genau wo das Auto ist."



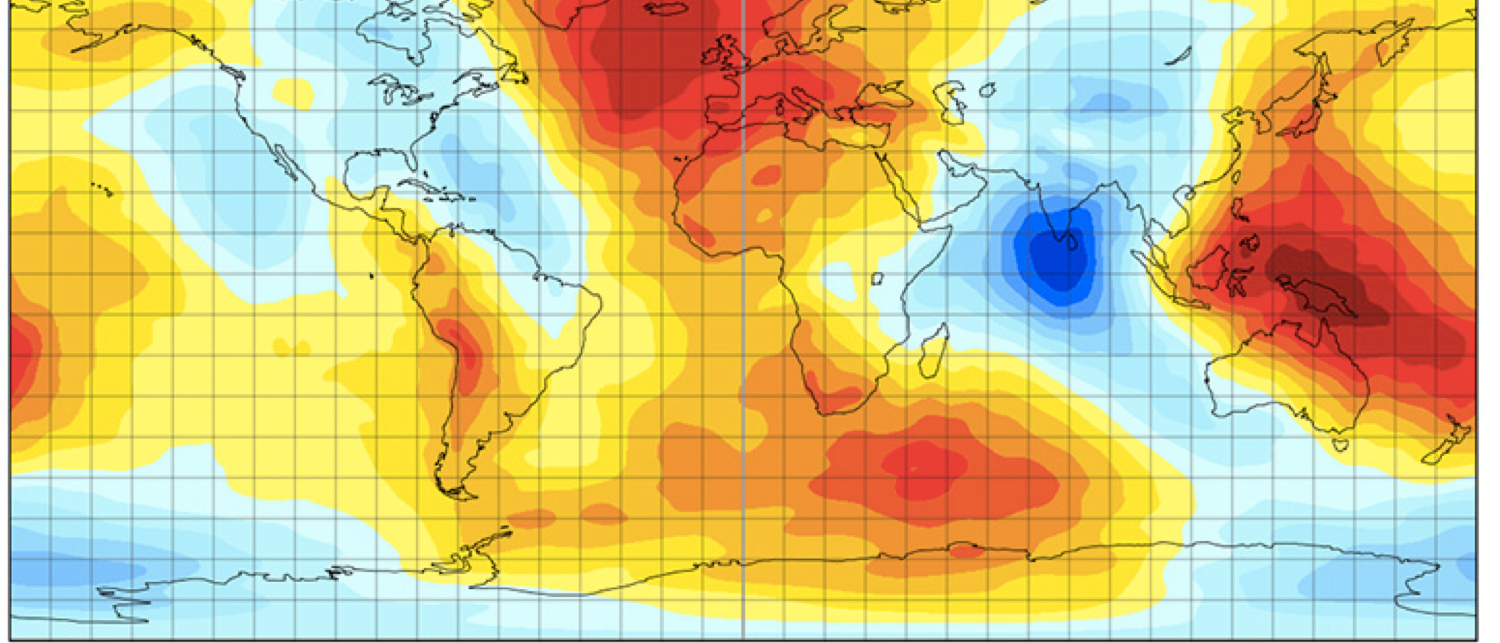© European Space Agency (Ausschnitt)
Woher die Schwerkraftdelle vor Indien stammt ↪  Spektrum.de

Die Musterlösung 

kursiv meine Kommentare zum Text.     

R + F:          Das hier ist unsere Erde – also, im Modell natürlich nur.
Die ↪ Erdfigur ist nun mal keine Kugel, insbesondere nicht bei Normalnull.

Richtig:       Auf der Erde steht das Auto mit dem Navigationssystem und weit über der Erde, da ist der Satellit im Weltall und dieser Satellit funkt ein Signal.

Annahme:   Das gilt nicht für fliegende Objekte, die auch mit GPS ihre Position bestimmen können. 

Richtig:       Und dieses Signal wird vom Navigationssystem empfangen. Das ist so ähnlich wie ein Radiosender allerdings nur für Navigationssysteme.

Richtig:       Und aus diesem Signal errechnet der Computer im Navigationssystem wieweit der Satellit vom Navigationssystem entfernt ist. 

F + R:          Das ist dann ungefähr, diese Strecke hier.
Es wird die ↪  Signallaufzeit gemessen. Das muss schon sehr genau sein. Eine einfache Überschlagsrechnung 10ns Fehler multipliziert mit 300.000 km/s ergeben schon 3m Abweichung.

Annahme:   Alle Satelliten und mein GPS-Empfänger haben die gleiche Zeit.
Das ist natürlich falsch. Insbesondere weil relativistische Effekte relevant sind.

Annahme:    Die Lichtgeschwindigkeit ist bekannt, aber leider in der Atmosphäre kleiner als im Vakuum. Und eine klare Grenze gibt es auch nicht.

Richtig:        Das Problem ist, damit weiß man noch lange nicht wo man auf der Erde ist. Denn es gibt auf der Erde ganz, ganz viele Orte, die genau dieselbe Entfernung zum Satelliten haben.

Falsch:         Hier auf diesem Kreis. Dieser ganze Kreis, Alle diese Punkte sind gleich weit vom Satelliten entfernt.

                    Der GPS-Empfänger ist auf der Kugeloberfläche des gemessenen Abstands.

F + R:          Deshalb gibt es einen zweiten Satelliten.

                    Klar gibt es einen Satelliten aber nicht deshalb. Schon aus Gründen der Logik (s.o.).

Folgefehler:   Und auch hier ist es wieder so: der Computer im Auto, der weiß ganz genau wie weit dieser zweite Satellit von dem Auto entfernt ist. Und auch hier gibt's wieder genau wie beim ersten viele, viele Punkte auf der Erde, die genauso weit von diesen Satelliten entfernt sind.

Falsch:         Und es gibt jetzt aber zwei Punkte, wo sich diese Kreise treffen. Die überschneiden sich da und das bedeutet: das Auto kann entweder hier an diesem ersten Punkt sein oder hier an diesem zweiten Punkt.

                    Die Schnittlinie zwischen zwei Kugeln ist ein Kreis, wenn sie sich überhaupt schneiden.

Folgefehler:   Um das zu finden, wo das Auto jetzt tatsächlich ist, gibt es einen dritten Satelliten. Und da passiert genau das gleiche: das Auto weiß ganz genau wie weit es von den Satelliten entfernt ist. Und natürlich gibt es auch hier wieder ganz viele Punkte, die diese Entfernung zum Satelliten haben.

R + F:          Aber es gibt auf der ganzen Welt nur einen einzigen Punkt, wo sich diese drei Kreise von diesen drei Satelliten treffen. Und genau das ist der Ort, wo das Auto ist.

                    Durch die Dritte Entfernung entstehen zwei Schnittpunkte zwischen den drei Kugeln. Einer ist im Weltall.

Falsch:         Und dieser vierter Satellit ist noch mal zur Kontrolle, dass alle Berechnungen richtig sind.

                    Der 4. Satellit dient der Zeitkorrektur. Denn die Entfernungsmessung läuft über die Signallaufzeit zwischen Satelliten und GPS-Empfänger. Und das ist nicht ↪  trivial - [2].

Richtig:       Dank der Satelliten 1-2-3-4, weiß der Computer im Auto ganz genau wo das Auto ist.


Natürlich habe ich in der Klausur nicht verlangt, dass ein Studierender das alles hinschreibt. Aber die zentrale Annahme es würde eine Schnittkurve mit der Erdoberfläche berechnet war natürlich notwendig.

Was soll´s

Ihr könntet sagen: "Ist ja nur für Kinder, dann ist es eben falsch. Erwachsene können das ja richtig recherchieren." ... "Au contraire mon amie!"

Viele greifen darauf als Erklärung zurück. Aber hier irrt die Maus. Ich kann mir gar nicht vorstellen, dass noch niemand bemerkt hat. Vielleicht ist das Experten einfach zu simpel. Ich hatte mal versucht, Kontakt mit der Redaktion zu bekommen. Brachte aber keine Reaktion. Und als Physiker sträuben sich meine Nackenhaare. Wir leben in eine vierdimensionalen Universum, also braucht es auch 4 Entfernungen [2], mindestens.

P.S.

Vereinfachen, ja immer. Simplifizieren, das ist gefährlich. Birgt es doch die Gefahr, dass entscheidende Inhalte verloren gehen. Das mit beschäftigt sich die Verständlichkeitsforschung, auch interessant.

Update 5.7.20

Sehr geehrte Damen und Herren,

ich bin ein Fan der Sendung mit der Maus. Die Sachgeschichten sind wirklich immer excellent.
Meinen Studierenden empfehle ist oft, dass Sie als Einstieg die passende Geschichte ansehen
sollen. Nun ist nichts ohne Fehler, das ist menschlich.

Die 2007 gedrehte Sachgeschichte zum GPS ist sehr nett aber leider grob falsch. Bereits
vor einige Jahren hatte ich daher versucht mit Ihnen Kontakt zu bekommen, leider erfoglos.
Eigentlich nicht rüberraschend, ein einzelner Professor an einer Provinzhochschule mit
geringer Reichweite relativ zur ARD. Das ist Ihnen eben egal.

Aber ist das ein valider Grund weiter Falsches zu verbreiten? Ich habe das in meinem Logistik-
blog (diese Seite) integriert: Bald ist Klausurzeit und die Aufgabe ist einfach gut geeignet, um das Verständnis der Studierenden zum GPS zu testen.

Heute, nein gerade eben, ist das Video wieder gelaufen. Hatte ich die Hoffnung, dass ein Update
kommen würde, so wurde ich enttäuscht. Schade, ober eigentlich im  Erwartbarem.

Beste Geüße,

Martin Wölker

Update 6.7.20

Von Maus <maus@wdr.de> Montag, 6. Juli 2020 07:59

Lieber Herr Wölker,

vielen Dank für Ihre Mail.

Leider können wir keine vorangegangene Mail mit Kommentar zur Erstausstrahlung des Beitrags von Ihnen finden.

Von anderen Zuschauern haben wir keinen Hinweis darauf bekommen, dass irgendetwas mit dem Beitrag nicht in Ordnung ist.

Wie Sie ja auf Ihrem Blog ja auch selber schreiben, ist es für unsere Zuschauer, die unsere Sendung ab Grundschulalter schauen, wichtig, Dinge vereinfacht und möglichst unkompliziert und nachvollziehbar darzustellen. Darüber hinaus stehen uns für eine Sachgeschichte in der Regel 6-8 Minuten zur Verfügung, um ein recht komplexes Thema darzustellen. Für alle unsere Sachgeschichten stehen uns auch immer entsprechende Experten zur Seite, die darauf achten, dass es trotz aller Vereinfachung zu keiner fehlerhaften Darstellung kommt.

Aber natürlich sind auch wir nicht immer fehlerfrei und prüfen gerne noch einmal, ob dieser Beitrag im Rahmen unserer Fragestellung einer Überarbeitung bedarf.

Darüber hinaus möchten wir Sie darauf hinweisen, dass das Einbinden unserer Beiträge auf andere Seiten aus rechtlichen Gründen nicht gestattet ist.
Gerne können Sie auf unsere Seite verlinken:

Für die Zukunft wünschen wir Ihnen alles Gute und wieder ungetrübten Spaß bei der Sendung mit der Maus.

Viele Grüße vom Maus-Team!

Von Martin Wölker, Montag, 6. Juli 2020 10:09

Sehr geehrte Damen und Herren,

herzlichen Dank für ihre schnelle aber unbefriedigende Antwort. Leider ist Ihre 
Antwort nicht namentlich gekennzeichnet, so dass ich Sie nicht ansprechen kann.

Aus der Beobachtung, dass Sie keine anderen Hinweise bekannt sind, schließen Sie auf die Richtigkeit der Videos. Nun vielleicht gab es Hinweise, die aber nicht verfolgt wurden und untergegangen sind. Zudem besteht kein kausaler Zusammenhang. In meinem Beitrag vermute ich, dass Experten so etwas vielleicht für zu Gering erachten. Mag sein oder auch nicht. Sicher aber ist, dass dieses Video in zahlreichen Kopien im Internet verbreitet wird. Durch die permanente Wiederholung steigt zwar nicht der Wahrheitsgehalt aber das Video wird glaubwürdiger. 

Sie heben ab, dass es ein komplexes Thema ist, das möglichst unkompliziert und nachvollziehbar dargestellt werden muss. Damit kämpft jeder Lehrende, egal in welcher Rolle er unterwegs ist. Nun zum einen ist GPS nicht komplex, da die Voraussetzungen komplexer Systeme nicht erfüllt sind, sondern nur nicht trivial, eben etwas kompliziert.

Aber genau hier sehe ich das eigentliche Problem. Zahlreiche Lehrer/Website/Blogs/Podcasts usw. 
benutzten das Video als (Unterrichts-) Material, womit sich die falsche Erklärung verfestigt. 
Ist das gut? Ich vermute, dass dies nicht Ihr Ziel ist.

Ich denke es ist leicht machbar den Sachverhalt auch Kindern korrekt darzustellen. Vielleicht war
2007 noch nicht die Zeit dazu, aber heute ist eine 3-D Animation kein ernstes Problem mehr. 
Aber das wissen Sie besser als ich. 

Auch weiterhin werde ich mich auf den Sonntag 11:30 freuen.
Egal was meine Kollegen von dem „Kinderkram“ halten.
Hoffentlich bleibt uns die Maus noch lange erhalten.

Martin Wölker

P.S. Danke für den Hinweis. Ich habe das geändert. Bitte schauen Sie mal rein, ob das für Sie so 

Von Maus <maus@wdr.de>  Montag, 6. Juli 2020 10:30

Lieber Herr Wölker,

nochmals vielen Dank für Ihre Rückmeldung.

Wir werden über Ihre Mail noch einmal in der Redaktionssitzung sprechen.Ob oder wann der Beitrag ggfs. geändert werden wird, können wir momentan leider noch nicht sagen oder Ihnen versprechen.
Ihre Kritik ist aber bei uns angekommen und wir möchten Ihnen versichern, dass wir sie sehr ernst nehmen.

Danke, dass Sie den Beitrag von Ihrer Seite entfernt haben. Sie hätten gerne direkt auf unsere Seite verlinken können, denn dort befindet sich der Beitrag ebenfalls:

Wir freuen uns, dass Sie uns auch weiterhin gewogen bleiben und senden 

viele Grüße vom Maus-Team!

Von Martin Wölker Montag, 6. Juli 2020 11:11

Liebes Maus-Team,

Die Maus-Seite und die Sachgeschichte sind oben im Text verlinkt.
Sehen Sie das bitte nicht als Kritik, sondern Sorge um die Glaubwürdigkeit.
Wenn sie einverstanden sind mache ich ein Update im Blog mit unsrem 
Mailaustausch. 

Viele Grüße,

Martin Wölker

P.S. Das Thema ist so interessant, dass ich gerne frage: „Spielt die Relativitätstheorie
        von Einstein in eurem täglichen Leben eine Rolle?“ Antwort: „Klar, GPS“

Von Maus <maus@wdr.de> Montag, 6. Juli 2020 11:48

Lieber Herr Wölker,

gerne können Sie unseren Email Austausch veröffentlichen.

Selbstverständlich nehmen wir Kritik auf und sehr ernst. So auch die Ihre. Und das auch die Maus schon mal so richtig falsch liegen kann und wie wir damit umgegangen sind, können Sie sich in dem Beitrag Geschenkband 2 anschauen:

Viele Grüße vom Maus-Team!


Quellen


[1] zahlreiche Quellen, auf jeden Fall Aktuelles googlen!

↪ Blogbeitrag – Marie Herberger, Klausureinsicht nach der Staatsprüfung - Wie man sich gegen das Prü­fung­samt durch­setzt, Legal Tribune Online, Wolters Kluwer Deutschland GmbH, Hürth, 22.02.2018

TU-Kaiserslautern, Einsichtnahme in Klausuren, Dokument der ⧉ Hochschule und Dokument vom ⧉ ASTA

Rechtlich:
↪ EuGH (20.12.2017 – C 434/16 Nowak vs Data Protection Commissioner) und
↪ § 29 BVwVfG Akteneinsicht durch Beteiligte

[2] Neben dem ↪ Wikipediaartikel hilfreiche Links

↪ wissenschaft.de – Thomas Bührke, Ohne Einstein kein Navi, Konradin Medien, Leinfelden-Echterdingen, 17. August 2015

↪ weltderphysik.de – Eberhard F. Wassermann, Navigieren mit Satellit: GPS, Deutsche Physikalische Gesellschaft, Bad Honnef, 11.11.2011

und ein Buch, das ich aber noch nicht gelesen habe:

Tobias Schüttler, Relativistische Effekte bei der Satellitennavigation: Von Einstein zu GPS und Galileo, Springer Vieweg, 1. Aufl., 30. Mai 2018 

Tobias Schüttler ist stellvertretender Leiter des Schülerlabors DLR_School_Lab am DLR Oberpfaffenhofen und promoviert am Lehrstuhl für Didaktik der Physik der Ludwig-Maximilians-Universität München.

Kommentare

Kommentar veröffentlichen